DOI: 10.1007/s11192-016-1940-3 | CITEULIKE: 14028879 | REFERENCE: BibTex, Endnote, RefMan | PDF ![]()
Hölyä, T., Bartneck, C., & Tiihonen, T. (2016). The Consequences of Competition: Simulating The Effects Of Research Grant Allocation Strategies. Scientometrics, 108(1), 263-288. doi:10.1007/s11192-016-1940-3
The Consequences of Competition - Simulating The Effects Of Research Grant Allocation Strategies
HIT Lab NZ, University of Canterbury
PO Box 4800, 8410 Christchurch
New Zealand
christoph@bartneck.de
Department of Mathematical Information Technology
University of Jyväskylä
Box 35, FI-40014, University of Jyväskylä, Finland
Abstract - Researchers have to operate in an increasingly competitive environment in which funding is becoming a scarce resource. Funding agencies are unable to experiment with their allocation policies since even small changes can have dramatic effects on academia. We present a Proposal-Evaluation-Grant System (PEGS) which allows us to simulate different research funding allocation policies. We implemented four Resource Allocation Strategies (RAS) entitled Communism, Lottery, Realistic, and Ideal. The results show that there is a strong effect of the RAS on the careers of the researchers. In addition the PEGS investigated the influence of the paper writing skill and the grant review errors.
Keywords: funding, allocation, competition, simulation
The PEGS software is available at: http://users.jyu.fi/~tiihonen/simul/fundingfun/simulation.zip
Introduction
Researchers are confronted with an environment of decreasing resources. Their competition for funding, publications, people, infra-structure, and promotions, is increasing steadily. The low acceptance rates for papers published at a conference or journal is even being used as indicators for their exclusivity. A conference with a low acceptance rate for papers is being advertised as a leading conference. Highly competitive grants are considered more prestigious than less competitive.
The National Institute of Health (NIH) had an acceptance rate in 2012, depending on the type of funding, of either 19.3%, 16.8%, or 16.3%, (National Institute of Healt, 2013). In other words, more than 80% of the proposals written for NIH are being rejected. The Engineering and Physical Sciences Research Council reported and acceptance rate within the financial year 2012-2013 of 34% (Engineering and Physical Sciences Research Council, 2013). The Royal Society of New Zealand revealed that their Marsden Fund had an acceptance rate of only 8% in the 2014 round.
England’s Economic & Social Research Council (ESRC) has faced an increase of applications of 33% between the years 2006 to 2010 (Economic and Council, 2010). This shows that the researchers are very actively seeking funding. ESRC funding, however, remained constant, which means that within the same time period the success rates of grants have declined from 26% to 12%. The Large Grants Scheme of the Australian Research Council (ARC) is generally regarded as a most prestigious source of research funding for Australian academics. Their success rates for grants hovers around only 22 per cent (Bazeley, 2003).
Geard and Noble (2010) developed a simulation for resource funding allocation. Their agent based competitive bidding system simulated four strategy variants. The results show that approximately three quarters of funding proposals are turned down. These numbers give rise to the concern about the time and effort spend on writing funding proposals. This does not only include the time of the applicant, but also the time for administrators to process the applications and the examiners to review the proposals.
One ironic consequence of this practice is that researchers have little to no time for actually doing research. In 2012, Australian researchers spent an estimate 550 years preparing 3727 proposals, of which only 21% were funded (National Health and Medical Research Council of Australia, 2013; Herbert et al, 2013). This does not even include time spent in administration or reviewing the proposals. This effort spent is equivalent to around 66 million Australian dollars. The total amount of funding actually allocated was 459.2 million dollars. To maintain the appearance that the process is efficient and effective it is necessary that the 66 million dollars remain invisible. They do not appear in any of the books of the funding agencies or the ministries. The motivation for funding agencies to make the funding allocation process more efficient and effective would probably be greatly improved if the costs for the writing of the proposals would also be charged to them. The justification often given for using such a wasteful process is that by allocating more money to the better researchers better results could be obtained. In case that a proposal gets funded it can also be used for the management of the project and possible publications. Some of the effort that went into the proposal writing can to some extend be recovered.
Frequent rejects are not limited to funding proposals. Researchers frequently have their papers rejected from journals and conferences. Only very few are able to maintain a consistently high publication records over longer periods of time (Ioannidis et al, 2014). In part this could be due to the lack of the papers’ quality, but it has also been pointed out that the review process in itself is faulty and that (almost) every paper that is written gets published eventually Bartneck (2010).
The career paths for academics are also increasingly scarce. The proportion of tenured staff in the USA has decreased from around 50% in the mid 1970s (Roey and Rak, 1998) to 21% in 2010 (Knapp et al, 2011). The dramatic increase in fixed term academics (Jones, 2013) influences this proportion. Similar behavior can be seen all over OECD-countries and Afonso (2013) concluded that “academia resembles a drug gang”. Funken et al (2014) pointed out that conducted an extensive survey on the situation of young academics in Germany and came to the conclusion that “No matter if professor, junior professor or research assistant, they all agreed that the intensive competition in the uni-directional German academic system has lead to an unbearable level of career uncertainty …In short, the increased competition is ruining the attractiveness of the Germany as an academic location.” Friesenhahn and Beaudry (2014) came to a similar result. Their study revealed that “Many young scholars shoulder extreme workloads to progress in their careers and to live up to what is expected from them.” Their first and most important recommendation is to increase funding for young researchers. The lack of career perspectives and structural disadvantages (van der Lee and Ellemers, 2015) make an academic career so unattractive that many women decide not even to try (Rice, 2014). Tertiary Education Unions around the world are deeply concerned about the situation for academics and the Templin Manifesto is a call for change (GEW, German Education Union, 2014). The constant exposure to rejections from funding agencies and publishers also has a negative effect that should not be underestimated (Day, 2011). Researchers who’s work has been frequently rejected might stop research work altogether. The Performance Based Research Fund (PBRF) in New Zealand even has a category for such academics: “R” for “research inactive”. Carayol and Mireille (2004) showed that such passive researchers significantly decrease the productivity of research labs.
This competition has reached a level at which considerable negative side effects start to emerge (Bartneck, 2010). Not only do the members of academia suffer from enormous stress (Herbert et al, 2014), job insecurity and lack of career perspectives, the funding system as it operates right now might not be the most efficient. In light of considerable costs of a competitive funding allocation Barnett et al (2013) suggested that it would be better to use a simple formula to distribute research funding. While one may or may not agree to this specific formula it still makes clear that there are alternatives to how resources are being allocated. We are not locked in to how the allocation is typically done right now. A reason for why change is coming slower than one would hope for is that even a small adjustment can have dramatic consequences for universities, and the careers of their researchers. The implementation of the changes can also take considerable resources. It would therefore be utmost desirable to be able to test different funding allocation strategies before implementing them.
In this study we will try to offer a simulation, called the Proposal-Evaluation-Grant System (PEGS). PEGS allows us to study what consequences different allocation strategies might have on the output of the research conducted and how sensitive these consequences are possible bias or inaccuracy in the selection. One of our goals has been to base our simulation on as much empirical data as possible. Furthermore, PEGS does consider psychological effects, such as the motivation of a researcher to write applications and publications.
1.1 Research question
Our main research question is what consequences different allocation strategies might have on the scientific output and the careers of the researchers. More specifically, there are several research allocation strategies (RAS) that deserve our attention. We gave each of them a name that exaggerates its nature:
- “Communism”, where every researcher gets equally resources every year without having to apply. The advantage of this scenario is that no time is wasted on writing, managing and reviewing proposals. A potential disadvantage would be that the grants given might be small.
- “Lottery”, where resources are distributed randomly between researchers. This scenario also does not create any overheads but larger grants can be given to a lucky few.
- “Capitalism”, where only the most capable researchers are intended to receive resources. This scenario resembles the status quo. It creates overhead but there is a tacit assumption that more resources can be given to the better researchers. We are interested to see to what extent the benefits of better allocation of grants outweight the overhead or tolerate errors in evaluation.
- “Idealism”, where no resources are wasted and no errors are made in allocating the funding to the most productive scientists.
In addition we are also interested in what psychological effect the funding distribution process has on the researchers. Is the funding game a self reinforcing cycle in which a few lucky researchers receive resources to become productive while most researchers become frustrated and stop researching?
2 Description of PEGS
PEGS is an agent simulation system that models individual researchers in their activities related to getting funding, aiming for promotions and making science. In addition we consider their interaction with the research organisation and its HR policy, the grant provider with its resource allocation scheme (RAS) and the scientific community that gives the ultimate valuation of the scientific output. In our context the main output of the simulation model is the “value” of the scientific output and the main input variable is the selected RAS. For the operation of the model we need submodels for researchers’ mental states and organisation’s personnel policy.
PEGS is a tool that allows policy makers and researchers to simulate simple peer review processes of funding agencies. The resource allocation procedure consists of researcher investing resources to writing application, funding organisation putting resources to evaluation and eventually allocating resources to the researchers. The simulated agencies have no memory about previous actions, meaning the model is static and there is no interaction besides receiving the current application and giving out the grants between the funding agency and the researchers. The real world is more complex, with social connections between the agency and researchers. Funding agencies might also consider the track record of a researcher to decide if he or she should receive another grant. Some grants even explicitly look at the track of a researcher, such as the NCI Outstanding Investigator Award (R35) award. To keep PEGS manageable we did not consider such effects, although PEGS can be extended in the future to accommodate such consideration.
PEGS models also the scientific output. Possibly the best base for assessing the scientific output is the publications that the researchers produce. At least 13 different bibliometric indicators exists to measure the productivity of researchers (Franceschet, 2009). For simplicity only the number of papers and citations is captured since it combines the the quantity and quality of the publications. In other words, the total number of papers and citations received are the parameter to be evaluated as a function of several factors. We acknowledge that the production of papers and the number of citations they attract differ considerably between different scientific disciplines but these differences will need to be tackled in a future version of PEGS.
In the following paragraphs we will introduce the various factors that PEGS is build upon. We realise that while PEGS is more complex than previous simulations, it will still be an abstraction of reality. Such abstractions are necessary since it is often not possible to attain empirical data upon which certain factors could be setup. Nevertheless, we hope to be able to show that PEGS is still able to provide valuable insights and that our abstractions are useful.
2.1 Time usage of researchers
Researchers have different kind of tasks within the organisation. Typically the responsibilities are divided into teaching, research and administration.
| Mean fraction of time | Total | Teaching | Research | Grants | Services |
| Full professor | 100% | 30.00% | 35.15% | 7.30% | 27.55% |
| Associate professor | 100% | 36.40% | 32.90% | 7.60% | 23.10% |
| Assistant professor | 100% | 31.50% | 40.10% | 11.60% | 16.80% |
| Post-doc | 100% | 10.00% | 60.00% | 20.00% | 10.00% |
Table 1 Average time allocation of researchers based on (Link et al, 2008)
Link et al (2008) provided a detailed analysis of how academics spend their time. Table 1 summarises their results. The column “Service” refers to activities such as administering/reviewing grants, advising students, paid consulting and all levels of service. The “Grants” column refers to the time used on writing the grant proposals. The assumption is made that 30% of the professor’s service time is used for administering grants. Post-docs would naturally not supervise grant writing, since there is no researcher at a lower position. Based on table 1 we conclude that academics at their different career levels use on average, 42.04% of their time for research. If they would spend no time on writing grants then this would be increased by another 19.75%. This percentage is the average grant writing time plus 30% of their service time. This means that if academics would not need to spend any time on writing grants then they would have on average 65.1% of their time available for research, assuming that they would have 3.31% administrative costs.
2.2 Grant system costs
To make the system time usage more accurate, there is also an administrative cost from having the grant proposal handling process. Administrative staff is hired for handling the funding proposals and otherwise these resources that are allocated for administrative staff, could be also used to research. The basic idea is that the amount of resources (time) that are allocated for administration is also lowered when the time for grant writing is lowered and when resources assigned to grant process is zero percent, also this administrative cost can be fully assigned for research.
To determine how much higher it should be as a reference, New Zealand's research quality evaluation system is used as an example (Tertiary Education Comission, 2012). Under the review system there are 6 757 researchers. The average hourly cost of researcher is $51 and yearly hours per one researcher are 1950. The PBRF runs every 6 years with a total cost of $50,750,200. So, the cost for each researcher is $1,251.80, or $24.5 per hour.
From here it can be seen that there is 3.31% overhead of the resources that would otherwise go to research. This means that researchers would have 3.31% more resources in use without PBRF which would go straight to research without application process. This includes also the time spent on reviewing the proposals. In England, similar system, called RAE, where administrative cost of this is 0.8% (Koelman and Venniker, 2011). This overhead is corresponding to research time; the less grant time, the less overhead. Eventually it can be assumed that when there is no grant system, all the overhead resources can be assigned for research time. Grants that are available through private sector are not in the focus of our simulation since their resource allocation process is often not documented.
2.3 Careers
PEGS includes a simulated academic career system. This is an important factor for the motivation of researchers and it can also influence how much time they can spend on research. The amount of time spend on teaching and administration varies amongst the different career levels. Education has a negative effect on research productivity. The more time researches spend on education, the less productive they are (Hattie and Marsh, 1996). We therefore need to define the different career levels and how they spend their time. In Australia, unlike the United States, but similar to Britain and New Zealand, the academic hierarchy had the following distribution (Moses, 1986):
- 9.3% of university teaching and research staff were professors,
- 12.3% were associate professors/readers,
- 32.1% were senior lecturers,
- 22.5% were lecturers,
- 6.0% were principal tutors, senior tutors/demonstrators.
The remaining 17.8% were tutors/demonstrators on contract who cannot compete in the promotion stakes. At the University of Canterbury, New Zealand, the distribution was in 2013 as follows (Canterbury University - Human Resource Department, 2013):
- 22% were full professors,
- 43% were senior lecturers,
- 17% were lecturers and
- 17% were post-docs
The feature that both sources have in common is that the shape of the organisation is like Grecian urn, where senior lecturers are the largest group. There is also evidence that in computer science field the number of post-docs has increased dramatically in the past few years (Jones, 2013). The assumption is that those positions prosper well where the grants are directed.
Only 7 out of 174 successful ARC applicants did have a principal investigator that did not at least have a Ph.D. degree. It is therefore fair to assume in PEGS that only research with a Ph.D. qualification or greater is examined. PEGS does not consider Ph.D. students as staff members and hence they are excluded from the career simulation although their contributions are visible through the increased output of researchers that received funding. Often funding is being used to finance Ph.D. students who then execute the proposed project. This leaves our simulated PEGS instance with four different academic positions: Post-doc, assistant professor, associate professor and full professor.
In order to get promoted, academics need to fulfil certain criteria before they are eligible for a higher position. Researchers are eligible to apply for promotion after a certain amount of years and a proven track record. Curtis and Thornton (2013) reported that in the 1990âĂŹs, a Ph.D. degree was on average obtained at the age of 31 and the first professorship was typically achieved at the age of 43.9. Moreover, he reported that fixed-term positions increased after the year 2000 and are now reaching over 40% of academic positions. Full-time permanent positions have decreased at a similar rate, plateauing to around 17%. A further distinction can be made between academics that are on a fixed term contract but who either have the option to receive a permanent contract in the future (tenure track) and those who will not have that option (non-tenure-track). Tenure-track positions have decreased to approximately 15%, while non-tenure-track positions have been plateauing around 15% for years.
The career level of a researchers has a strong influence on how they divide up their time on the main academic activities of research, eduction, services and grant writing. The differences in time allocations between researchers are shown in table 1.
At times researchers may also decide to leave academia. The factors that contribute to such a decision are salary, integration, communication and centralisation (Johnsrud and Rosser, 2002). Their study showed that career opportunities within academia also affects job satisfaction, morale and commitment. Furthermore they found that neither gender nor ethnicity does significantly influence changes in morale. Barnes et al (1998) presented similar factors as mentioned above, but distills them to two main predictors; frustration due to time commitments and lack of a sense of community. Especially researchers who have not gained a permanent position are likely to leave research organisation, if they have received offers elsewhere. In this case a single interview of an anonymous frustrated colleague was used as a guideline (who mentioned that a researcher would wait seven years for a tenure until leaving an organisation). PEGS condensates the factors even further by focusing on frustration which is dependent on two main predictors, level of research funding and recognition gained through promotions. Even academic careers come to an end although the retirement age varies considerably between countries and professors. Some continue working well beyond the point when they are eligible for retirement.
Bazeley (2003) showed that receiving a grant is dependent on the university that researcher is representing, as well as it is dependent on the academic’s status; having a research-only position had a strong positive correlation with the success in winning funding. Research fellows and readers are more likely to be successful on average than teaching and research academics at an equivalent level (Bazeley, 2003). The average retirement age is set to 67, and it is expected for researchers to gain their Ph. D. at age of 30, on average.
2.4 Motivation
There have been various studies which tried to identify the factors that influence the researchers’ productivity. Kelchtermans and Veugelers (2005) pointed out that these factors include gender, age, education, rank of the university, talent, luck, effort, tenure, rank, and seniority in rank. We speculate that further factors such as courage, intelligence, writing skill, charisma, social contacts and determination may play a role. Moses (1986) investigated the relationship between rewarding academic staff and their motivation. The results show that MaslowâĂŹs hierarchy of needs also seems to apply to academia. First of all safety, meaning having a permanent position, increases motivation. But also the sense of achievement, such as recognition for teaching, promotions, supervision of students, published papers and successful grant applications increase motivation. But the opposite is true as well. Lack of these recognitions is causing demotivation (Day, 2011). Grit does also seem to have a major effect on academic success (Duckworth et al, 2007).
Motivation is also associated with the intention of researchers to leave academia. Barnes et al (1998) showed a model in which the intent to leave academia dependent on four predictor variables (stressors): the reward and recognition, time commitment, influence, and student interaction. Furthermore it depended on two moderator variables: Interest in discipline and sense of community. They showed that there is a positive correlation between stress and intention to leave academia. From the four stressors, time commitment had the strongest correlation for intention to leave the academia.
2.5 Skill
The assumption is that researchers are individuals, hence not possessing the same weaknesses and strengths, such as their research skills. Characteristics and factors that are frequently mentioned in the literature (Barnes et al, 1998; Link et al, 2008) are:
- personal properties (talent, skill, intelligence)
- career-centered attributes (tenure, seniority)
- effort (motivation, determination, stress)
- time (available in total, used for applying, used for research, used for teaching)
Geard and Noble (2010) presented a model where they define a few attributes such as research skill R which is distributed uniformly between 0 and 1. There is also the attribute G which increases the researchers’ scientific output if a grant is awarded. Researchers also have an attribute called effort. If they apply for a grant, this application time is taken away from actual research time. A few assumptions are also made: The quality of researchers’ application correlates with their research skills. However, researcher can compensate lower research skill with using more time for applications, and for this there is a diminishing returns on time invested. Also, the funding decision is not accurate, hence there is a noise factor allocated. For PEGS, a similar method for skill allocation is used, but instead with a log-normal distribution that mimics the observed distribution of the scientific impact.
Even when the applicant might be an expert on his/her field, it is not obvious that the grant reviewers are. In other words, the grant application needs to be composed in a manner where the idea can be sold to the person with lesser knowledge about the subject. Hence it is not obvious that a talented researcher is also a talented application writer (Peyton and Bundy, 2006), a new factor, application skill, is also introduced in PEGS.
There is a small correlation between gender and productivity. Females tend to publish less at the beginning of their career compared to males but this reverses later in their careers (Kelchtermans and Veugelers, 2005). van Arensbergen et al (2012) showed that the link between gender and productivity disappeared in the younger generation. Furthermore, there seem to be a quadratic relationship between age and number of publications. Besides the established correlations that is likely also an element of chance. At times papers get accepted or rejected not because of their quality but possibly because of the specific reviewers that were assigned. We therefore included a stochastic element into our simulation.
Another important factor for the productivity of a researcher is their career status. Researchers in higher positions typically have a higher output. Link et al (2008) showed that despite the fact that senior researchers are increasingly burdened with administrative tasks, they also supervise many postgraduate students. Instead of performing the research themselves, their students and post-docs do. The senior research maintains his authorship role while not being directly involved in the execution of the studies. In extreme cases this is considered trophy authorships.
Researchers also develop a skill of writing proposals and possibly even enter a self reinforcing cycle. Researchers who received grants before are way more likely to receive again. Only 4.1% of funded researchers did not have any funding during the previous three years. When it comes to publications, successful ARC applicants have been solo or first authors for more books, articles and chapters than unsuccessful ones (Bazeley, 2003).
Among ARC, the median age for grant applicants ranged from 40 to 49 years. Younger applicants (below 40 years) who applied either by themselves or who were the first author of the application tended to be less successful than those who were older (Bazeley, 2003). However, grant applications with a young researcher as second or third named investigator were at least as successful. Male researchers receive more grants, which can be explained by the lack of senior female researchers. Bazeley (2003) indicate that that there is no significant difference either in age or gender on the success rate of applications.
2.6 Scientific impact
Scientific impact means how well the work has been received among its target audience compared to others. Shortly put, how often the paper has been cited. Wang et al (2013) presented a validated model based on empirical data that can predict the citation patterns: How often, and when the citations occur. For a mechanism to count citations of a single paper pj as a function of time the following formula is presented for probability that paper i is cited at time t after publication as
$$\prod_i\left(t\right)={\eta{}}_ic_i^tP_i\left(t\right)$$where \({\eta{}}_i\) indicates fitness of the paper \(c_i^t\) indicates received citations so far, and \(P_i\left(t\right)\) aging as a function of time.
2.7 Discussion
From the above elaboration we identify several factors that influence the success in grant applications and in science itself: fairness and competitiveness of the grant allocation scheme, available time, career system, personal properties, motivation and finally the citation mechanism of the scientific community. These can be roughly divided in grant allocation policy, organisational policy and personality related aspects.
On grant allocation policy level the following aspects should be taken into the model:
- Total amount of research resources (compared to the potential/desire of the researcher population to use them).
- Distribution of resources (varying between flat (communistic) distribution and dichotomic distribution to selected grant holders only)
- Grant selection objectivity (ranging from lottery to perfect, objective ranking of applications)
- Application evaluation criteria (weighting between research and writing merits of the application)
- The application evaluation overhead.
As our focus is in grant allocation policies we model only one discipline in one organisation. Hence the essential mechanism on organisational level is the promotion policy (leaving aside science policy and competition between different organisations).
On researcher level we assume, for simplicity, that the personal properties, such as skill to write proposals or papers, are constant in time for each individual. Moreover, we consider each researcher for her individual work only (ignoring collaboration from the model). For motivation we build a simple model for temporal dynamics which we assume the same for all individuals. Thus we have to model essentially
- Variability in skills among researchers and role of skills in creation of scientific impact
- Personal productivity (mechanism that explains the amount of papers for given resources).
- Model for factors of productivity (weighting the roles of frustration and availability of resources to productivity)
- Build up of frustration due to lack of promotion or funding.
- Applying intensity (how much effort is spent in application writing and how it depends on the personal status)
We will now proceed in describing the exact mathematical model that is used for PEGS.
3 Mathematical Model
PEGS is based on several assumptions that we will now discuss. First, we consider a population of researchers as a pool of decision making agents. They have to split time to apply for funding, to make science, to teach and to provide other services. The scientific output will be primarily papers whose quantity depends on the time available and motivation to research. The quality/value of publications depends on the individual research skills. The researchers also have careers and frustration levels which are interconnected. Rejection either in funding or promotions increases frustration. Secondly, we assume that publications are a good indicator for scientific output. Researchers might also have other outputs, such as contributions to the community and patents, but for simplicity we focus on publications. The simulated PEGS does not include a sub-model for the peer-review process for publications.
Our modelling goal is to measure the influence of different grant distribution policies to a research community and its scientific impact. As different communities are typically observed with yearly statistics we build a discrete in-time model with a time step of one year. The main observable will be yearly accumulated citations to the scientific output and the main input parameters to be varied are related to the allocation policy for research grants. Other model parameters and observables are related to different structural components and submodels of the overall system (like HR-policy, dynamics of motivation/frustration and its influence to research productivity, distribution of research skill and so on).
3.1 Dependency of variables
Before introducing the concrete variables and their dependencies, we introduce the notation conventions. We will refer to sets with uppercase, to individual items (set members) by lower case. The main concepts are organisation \((o)\), paper \((p)\) and researcher \((r)\). In general the functional dependencies are stochastic. So by \(f\) we refer to a generic stochastic function. By \(y\) we refer to an individual year.
The model contains dependencies between multiple elements. The modelled process involves funding to researchers that work in an organisation and produce publications that are valued for their scientific impact. We elaborate the model backwards starting from the observed output.
We will elaborate separately on the variables related to the dynamics of an individual (researcher, his/her personal state, papers and citations) and the status of an organisation (movement of researchers in and out and between different career levels). Finally we will consider the variables necessary for the resource allocation as grants.
3.2 Researcher and paper dynamics
We fix as the main output parameter of the simulation the amount of yearly citations to the papers produced by the organisation \(o\). That is, the cardinality of the set
$$C^o(y)=\bigcup_{p\in{}P^o(y)}C(p,y)$$where \(C(p,y)\) contains all citations \(C\) of the paper \(p\) in the year \(y\). This does not include the citations of resigned/retired ex staff that is often included in standard bibliometric comparisons. The (active) publications of the organisation in year \(y\), \(P^o(y)\), is defined as follows:
$$P^o\left(y\right)=\bigcup_{r\in{}R^o(y)}P^r$$where \(P^r\) is the set of publications by researcher \(r\) and \(R^o(y)\) is the set of researchers of the organisation \(o\) for the given year. Citations per researcher are needed in career path modelling and formed as follows:
$$C(r,y)=C(r,y-1)+\sum_{p\in{}P^r}C(p,y)$$We now need to describe how the citations of the publications emerge and how the number of publications can be calculated. Let us start with defining how the publications attract citations. The formation of citations is a function of the quality of paper and time since publishing, since the citations are not formed in one instance but over the time.
$$C\left(p,y\right)=C\left(p,y-1\right)+f\left(y-y_p,q(p)\right)$$where \(y_p\) is the year of publishing, and \(q(p)\) indicates the quality of publication. The quality is formed as a function of researchers skill \(s\):
$$q\left(p\right)=f\left(s(r)\right) \qquad \text{for } p \in P(r)$$The number of new publications during a year \(y\), is a function of time available for research\(\tau_r\) and researchers productivity. This, of course, is measured for year \(y\):
$$card (P_r(y)) = f(\theta_r(y), \tau_r(y)) $$The productivity \(\theta{}\) consists of two parts, resource dependent productivity (depending on funding decision) and commitment (which depends on promotion history):
$$\theta{}(y)=f\left({\theta{}}_b(y),{\theta{}}_m(y)\right).$$Here \(\theta{}_b\) is the commitment, which is dependent on the frustration \({\theta{}}_b(y)=f(u_r,y)\) and \({\theta{}}_m(y)=f(m_w, m_r,y)\) is a function of expected resources \(m_w\) and received resources \(m_r\).
The decision making of the researchers is modelled with the concept of frustration that influences the productivity of a researcher and tendency to seek opportunities outside of academia. We assume that frustration evolves as function of funding decisions and promotions. Frustration builds up over time and hence is modelled incrementally as:
$$u_r\left(r,y\right)=f\left(u_r\left(r,y-1\right),a,p,r,m_w,m_j)\right)$$where \(r\) is researcher, \(a\) years in academia and \(p\) is position. This is dependent also from how many resources were wanted \(m_w\) and received \({\ m}_j\) for year \(y\).
Time available for research depends from the funding \({\tau{}}_e\), available for all the researchers, funding received through grants \({\tau{}}_g\) and the resource used in applying for grants \({\tau{}}_a\).
$${\tau{}}_r\left(r,y\right)={\tau{}}_{e}+{\tau{}}_g\left(r,y\right){-\tau{}}_a\left(r,y\right).$$Time used for applying, \({\tau{}}_a\) is dependent on the level of frustration \(u_r\) and from the position \(p_r\).
$${\tau{}}_a(r)=f\left(p_r,\ u_r,r\right)$$3.3 Organisation dynamics
To understand the differences between position ladders \(p_r\), the dynamics of the organisation need to be opened.
First we will define how researchers join or leave academia. The set of researchers of an organisation during year \(y\),\(R^o(y)\) evolves as function of time as follows:
$$R^o(y) = R^o(y-1) \backslash L(y) \cup J(y) $$where \(L(y)\) is the set of researchers leaving the organisation and \(J(y)\) is the joining researchers at year \(y\). Researcher leaves from organisation if either the frustration \(u_r\) grows too large or the time spent in academia a grows too high which is considered as exceeding the retirement age. More formally:
$$r \in L(y) \text{ with probability } f(u_r, a, y).$$Joining to organisation depends on the HR policy of the organisation. On general level we assume that the amount of new staff is dependent on the current staff volume and of the vacancies becoming free:
$$card (J(y)) = f(card(R^o(y-1), card(L(y)) )$$That is, the amount of new recruitments depends (at least stochastically) on the current head count after resignments.
Whether researcher gets promoted depends on the researcher related attributes like citations \(c^r\), years spent in academia a, researcher’s current level \(l\) as well as organisational attributes like positions available on next ladder and performance of the peers at current level. This results in:
$$l(r,y)=f\left(l\left(r,y-1\right),a\left(r,y\right),\ c\left(r,y-1\right)\right)$$The positions that are available for given ladder do not have to be fixed. This way the promotions can depend mainly on researcher’s personal traits, not just from chance of opening of new positions in right time.
3.3.1 Grant allocation
The quality of applications is dependent on the researchers’ personal traits and how much time they allocate to prepare the application.
$$A(r, y) = f(\tau_a(r,y), m(r,y), s(r), w(r))$$where \({\tau{}}_a\ \) is time used for applying, \(m\) is motivation, \(s(r)\) is research skill and \(w(r)\) is applying skill.
The grant applications are reviewed with limited resources, hence the perceived quality of the application at evaluation, \(E\), depends of the actual quality and the time available for assessment \(\tau_o\),
$$E = f(A, \tau_o).$$Resources for research consist of two parts: resources distributed uniformly among researcher population \(R^o\), and to resources distributed as competitive grants based on the perceived quality of researchers’ applications. The amount of grant funding \({\tau{}}_g(r)\) received by researcher \(r\) is dependent on quality of the application \(\ A_s\), when it is compared to quality of other researchers applications.
$$\tau_g(r) = G(E(R);r)$$where \(G\) is the grant allocation function taking all evaluated applications as arguments, such that
\[\sum_r \tau_g(r) = cnst\]4 Simulated model instance
Now that we have described the factors of PEGS, we can describe a concrete instance of the model to be simulated.
Since we are interested in the distribution of limited resources using different policies we set the total amount of funding available as constant over the years and across different simulated scenarios although the literature (Afonso, 2013; Economic and Council, 2010) indicates that the amount of resources available for research has decreased over the years.
The main aspects that influence how the resources get allocated are related to application writing and evaluation and actual distribution of resources amongst the researchers.
4.1 Citations
We use a formula derived from equation (1) to count citations of a single paper \(p_j\) as a function of time. The probability that paper \(i\) is cited at time \(t\) after publication is given as:
\[c_i^t=m\left(e^{\frac{\beta{}{\eta{}}_i}{A}\Phi{}(\frac{\ln{t-{\mu{}}_i}}{{\sigma{}}_i})}-1\right)\]where \(\Phi{}(x)\) is the density function of the normal distribution, \(m,\ \beta{}\) and \(A\) are global parameters and relative fitness is presented as \({\lambda{}}_i\equiv{}\ \frac{\beta{}{\eta{}}_i}{A}\). \({\mu{}}_i\) indicates \(immediacy\), governing the time for a paper reach its citation peak and \({\sigma{}}_i\) is \(longevity\), capturing the decay rate (Wang et al, 2013). \(t\) indicates time since publication in years.
In our case the immediacy, longevity and m are set to constant values 1.0 and only the fitness will vary. Hence simplifying the equation (20) and assuming that the citations are created by a Poisson process we get
$$c_i^y=Poisson(e^{\lambda_i \Phi{}(\ln{(y-y_p)}-1)}-1).$$Naturally the fitness should depend on researcher skills.
4.2 Researcher skills
The empirically observed distribution of the papers' fitnesses by Wang et al (2013) suggests lognormal distribution for \(\lambda\). This invites us to set the fitness as \(\lambda_i = s_rf\) where both the personal research skill \(s_r\) and the per paper variability \(f\) are drawn from lognormal distributions. We fix the variance of \(\log(\lambda)\) to \(0.25\) and split this variance between \(\log(s_r)\) and \(\log(f)\) with simulation parameter \(c_{skill}\).
4.3 Publications
The number of papers \(P\) a researcher publishes (see function 3) in year \(y\) is defined by the formula:
$$P(y)= Poisson(\tau{}_y*c_{publ}*((1-c_{prod})+\theta{}_y*c_{prod}))$$where \(\theta{}\) is the productivity and \(\tau{}\) the time available for research. The calibration constant \(c_{publ}\) is used to adjust the yearly publication rate under fixed productivity and \(c_{prod}\) can be used to adjust the relative importance of motivation and funding related productivity. In simulation \(c_{publ}\) is kept inversely proportional to the total research resource to normalize the expected publication count to one publication per researcher per year for \(c_{prod}=0\).
4.4 Productivity
As in equation (8), commitment is created with formula \({\theta{}}_b=1-u_r\), where \(u_r\) is current frustration. Resource productivity \({\theta{}}_m\) in its turn depends on how much resources was expected, and how much was received. The relative importance of commitment and resources can be adjusted in simulations by parameter \(c_{commit}\). More formally:
$$\theta{}={\theta{}}_b+{\theta{}}_m=c_{commit}*\left(1-u_r\right)+(1-c_{commit})*max\left(1,\frac{m_r}{m_w}\right)$$4.5 Frustration
Frustration is dependent on resources and promotions. The formula is as follows:
$$u_r\left(r\right)=u_r^m+u_r^p$$For evolution of monetary frustration two mechanisms are considered. First mechanism is monotonous build up of frustration due to limited amount of funding. This is normalised so that with average funding level full frustration is reached in\(1/c_{frus1}\) years. The second mechanisms reduces or increases frustration in case the grant is bigger or smaller than the average for the researcher population. That is: with \(m_w\) as the (subjectively) expected resources, \(m_r\) the actually received resources and \(\bar m\)the average resource per researcher
$$u_m(y) = \max(0, u_m(y-1) + (\frac{m_w}{m_w-\bar m})\left(1-\frac{m_r}{m_w}\right)*c_{frus1} + c_{frus2}u_2(m_r))$$where
$$u_2(m_r) = \frac{\bar m -m_r}{1 -\bar m} \text{ if } m_r > \bar m,$$ $$u_2(m_r) = \frac{\bar m -m_r}{\bar m} \text{ otherwise.}$$ Here \(c_{frus2}\) is a simulation parameter controlling the importance of this effect. The mechanism is normalised to be independent of the amount of resources available.The promotional frustration depends on how much time researchers spend on each position. If the expected time for promotion has passed the frustration starts to grow:
$$u_p(y) = c_l*max(0, t-T_l)$$where \(t\) is the time spent in the position, \(c_l\) is the yearly increment in frustration (depends on position level l, c\(c_l = (0.2, 0.2,0.125, 0)\)) and \(T_l\) is the time in position where frustration starts to grow in position level l,\(T_l = (3, 3, 4, -)\)).
4.6 Human resource issues
The personnel status of an organisation is updated yearly as follows: first the persons retiring or leaving due to excess frustration are removed from population. Then, starting from the highest level of positions (professors) promotion from the previous level is processed. Once all promotions have been executed, new staff is taken to the first position level.
For our simulation we use four levels for positions: \(l=\{1,2,3,4\}\), which can be taken as {post-doc, assistant professor, associate professor, full professor}, respectively.
The researcher leaves due to frustration if the level of frustration \(u_r\) exceeds one.
$$u_r \geq{} 1, r \in L(y)$$When researcher has spent long enough (at least \(32\) years) in the organisation the probability of retiring that year will be positive (0.25 in simulations leading to expected retirement after \(35\) years of service).
For promotions two extreme scenarios are implemented: position structure based and researcher performance based. In both scenarios the researchers on level \(l-1\) are filtered for promotion to level \(l\) starting from the highest level.
In position structure based scenario the head counts on each level are fixed. Hence the number of promotions is determined from resignations and promotions on the higher level. The researchers are sorted according to citation count within each level and the top of the list gets promoted.
In researcher performance based scenario a researcher gets promoted if she has been working a minimum time in current level and shows good enough performance compared to peers on same level. That is, has at least \(c_r(y) > c_{prom} \bar c\) citations where \(\bar c\) is the average citation count of researchers on the same career level. Value for the threshold constant \(c_{prom}\) is used as simulation parameter
In both scenarios, both the promotional and monetary frustration of researcher go to zero when promoted. Finally, once all promotions have been done, new post-docs with random research and writing skills are created to the first level to restore the organisation head count.
4.7 Quality of grant application
The quality of researchers’ grant applications depends on their research and applying skills and motivation. Dependency model with a tunable parameter \(c_{res}\) will be considered:
$$Q=c_{res}s_r + (1-c_{res})s_a(1-u_r)$$where \(s_r\) is the research skill, \(s_a\) the applying skill and \(u_r\) the frustration.
The evaluated quality \(Q_e\) of the application depends on the actual quality \(Q\) and evaluation error \(E\). As there is no empirical data on the type of evaluation error and its dependency on the resource spent in evaluation (overhead) we consider a simple model with tunable error term:
$$Q_e=(1-c_{err})Q+ c_{err}e,$$where \(e\) is random error with same distribution as the application quality.
4.8 Resource allocation
Resource allocation to research is made in several phases. First the nominal total research resource level \(\tau\) is fixed and productivity and frustration mechanisms normalised. The total resource is divided to overhead, evenly distributed resource and resource available for grants, \(\tau = \tau_o+ \tau_e+ \tau_g\) as dictated by the simulated scenario.
For Communism \(\tau= \tau_e\), for Lottery and Ideal scenarios \(\tau=\tau_g\).
In Capitalism (a.k.a. Realistic) scenarios the resource used for application writing is computed as a fraction of the evenly distributed resource (to enable all researchers to allocate time in application writing). The time spent in application writing is proportional to motivation, \(\tau_a=c_{write}\tau_{e}(1-u_r)\), where \(c_{write}\) is a simulation parameter.
5 Simulation
5.1 Simulation setup
The simulation was set up to study the equilibrium behaviour of the academic community under fixed grant allocation policy. Hence only one organisation was implemented to model the whole community. After preliminary tests it was found that population size of 100 researcher or bigger is needed to eliminate the artifacts due to population size. Hence the nominal population size of 100 was chosen for experimentation. A warm up time of 100 years was found sufficient to eliminate the effects of initial values. Simulations were performed as one long run of the model taking independent samples at regular intervals.
5.2 Comparison of grant allocation policies
A set of experiments with rather diverse allocation scenarios was made to compare different grant allocation policies. We considered pure communism (all resources distributed evenly) and scenarios where half of the resources were allocated evenly and the rest as grants based on either pure lottery, ideal oracle-like selection (all resources for the most skilled researchers without any cost of writing or evaluation) and realistic scheme with cost of application writing and significant role for writing skills and evaluation error (equal weight for research and writing skill in quality of application and equal weight for the quality and random error in selection).
Four contextual parameters were varied in addition to the grant allocation policies:
- level of resources (50% to 60% of the full capacity of the researcher population),
- frustration build up mechanism (only monotonous build up of frustration due to limited funding or with additional effect due to comparing to the peer average funding level),
- variability in researchers’ skill levels (35% or 65% of the variance in papers’ fitnesses attributed to differences between researchers, the rest being random variation in the output of an individual),
- promotion policies (personal promotion after sufficient years of service and sufficient citation record or based on availability of free positions on next ladder within a rigid position structure).
We monitored the citation and publication counts, as well as average skill and frustration levels and the average yearly resignations/recruitments. These are summarised in Table 2 and Figure 1 detailing only the effects of grant allocation and promotion policies.
| Promotion | Case | Citations | Papers | Frustration | Skill | Recruitments |
| Individual | Communism | 345 | 82 | 36 | 113 | 3,8 |
| Individual | Lottery | 351 | 84 | 38 | 113 | 4,4 |
| Individual | Realistic | 403 | 80 | 34 | 120 | 5,1 |
| Individual | Ideal | 535 | 89 | 39 | 126 | 7,3 |
| Organizational | Communism | 338 | 81 | 38 | 115 | 4,3 |
| Organizational | Lottery | 342 | 84 | 39 | 113 | 4,8 |
| Organizational | Realistic | 398 | 80 | 34 | 119 | 5,1 |
| Organizational | Ideal | 514 | 90 | 38 | 122 | 6,5 |
Table 2 Publication, citation and recruitment rates/100 researcher years and accumulated frustration and skill levels
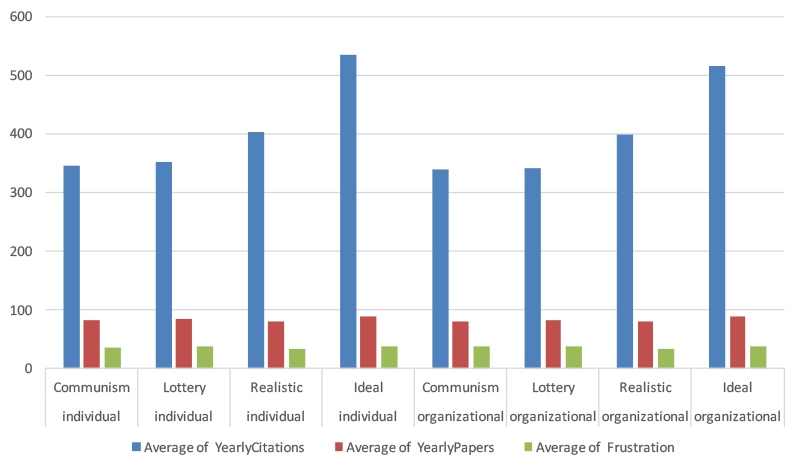
Fig. 1 Publications, citations and frustration across RAS and Promotion type
We performed an ANCOVA in which the RAS and the Promotion Policy were the independent variables and Frustration Speed, Skill Parameter and Level Of Resources were covariants. Citations, papers, frustration and skill were the dependent variables. The RAS had a significant influence on Citations \(F(3,629)=3474,141, p<0.001\), Papers (\(F(3,629)=4600.075, p<0.001\)), Frustration \((F(3,629) = 639.942,p < 0.001)\), and Skill (\(F(3,629) = 1179.250,p < 0.001\)). Post-hoc t-tests with Bonferroni corrected alpha showed that that all four RAS were significantly different for almost all dependent variables with the exception of the ideal and lottery RAS were not significantly different on Frustration and the RAS lottery and communism were not different in terms of Citations.
The Promotion Policy had a significant influence on Citations \((F(1,629) = 53.044,p < 0.001)\), Papers (\(F(1,629) = 9.344,p = 0.002\)), Frustration (\(F(1,629) = 8.992,p = 0.003\)), and Skill (\(F(1,629) = 31.346,p < 0.001\)). There was a significant interaction effect between RAS and Promotion Policy on all dependent variables.
Frustration Speed had a significant influence on Frustration (\(F(1,629)=5.923, p=0.015\)), Papers (\(F(1,629) = 77.074,p < 0.001\)), and Citations (\(F(1,629) = 9.608,p = 0.002\)). The Skill Parameter had a significant influence on Citations (\(F(1,629) = 1534.39,p < 0.001\)), Papers (\(F(1,629) = 19.587,p < 0.001\)), Frustration (\(F(1,629) = 24.506,p < 0.001\)), and Skill (\(F(1,629) = 3796.045,p < 0.001\)). The Level of Resources had a significant influence on Citations (\(F(1,629) = 37.752,p < 0.001\)) and Skill (\(F(1,629) = 10.059,p = 0.002\)). It did not affect the level of frustration and papers (indicating that scaling of frustration mechanism and paper production mechanism worked as expected).
The communism and lottery scenarios differ only in the way each researcher gets the expected research funding. Communism guarantees constant low level of funding that results to constant increase of frustration whereas lottery leads to fluctuating funding and staircase type of evolution in frustration. This difference is enough to have an impact in the personnel dynamics and paper productivity. Lottery creates unlucky individuals that frustrate faster and also resign faster than in communism (resignations from level 1 are one year earlier on average in lottery compared to communism and the level of dropouts is over 10% units higher (18 % vs 5%)). This results in higher volume of recruitments and higher proportion of level 1 staff for lottery. Lottery creates also a subpopulation of lucky ones that get funded and hence produce more papers, attract citations faster and get promoted earlier. This makes the frustrated unlucky ones overrepresented in the population and increases the population level frustration. The chance element in lottery helps lucky less qualified individuals to promote which slightly reduces the population skill average compared to communism. The sum effect of all these mechanisms is that the differences in citation counts are not significant between communism and lottery, despite differences in other observables and population dynamics.
Compared to "blind" communism or lottery the ideal and realistic schemes that account for research skills lead to higher average skill in population, faster circulation of staff and to higher citation counts. The time spent in writing leads to smaller average paper count while ideal allocation of funding improves productivity by allocating funds mainly to motivated researchers. The differences between grant allocation policies are bigger than between quite different promotion policies. Other factors (frustration build up, level of resources and variability in skill levels) have also statistically significant effect to most observables but these are as a rule smaller than the effects between grant allocation policies. In particular they do not alter qualitatively the effects shown here for the citations. However, especially the variance in skill levels among researchers has a clear influence to the difference in citation counts between the skill based and random allocation scenarios.
Individual promotion policy allows, and leads to, varying personnel profiles. As we can see from Table 3 the grant allocation schemes have significant impact to the individual promotion and head counts on different career levels. The impact of allocation schemes is clearly much bigger than the effect of different skill distribution in the basic population. For fixed personnel structure (25 persons for each level for all time) the differences were best observed in varying promotion ages. Skill (as well as luck) based allocation of funding leads to faster promotion.
| SkillParameter | Case | 1 | 2 | 3 | 4 |
| 0,35 | Communism | 18,8 | 21,8 | 32,5 | 27,0 |
| 0,35 | Lottery | 21,0 | 22,0 | 31,7 | 25,3 |
| 0,35 | Realistic | 25,6 | 24,0 | 28,7 | 21,8 |
| 0,35 | Ideal | 34,3 | 25,1 | 23,9 | 16,6 |
| 0,65 | Communism | 19,8 | 22,6 | 32,1 | 25,4 |
| 0,65 | Lottery | 22,0 | 22,9 | 31,1 | 24,1 |
| 0,65 | Realistic | 26,5 | 24,9 | 28,4 | 20,2 |
| 0,65 | Ideal | 35,8 | 24,8 | 23,9 | 15,5 |
Table 3 Average head counts at different career levels (individual promotion policy)
| Case | Level 1 | Level 2 | Level 3 |
| Communism | 5,3 | 10,8 | 19,9 |
| Lottery | 4,9 | 10,3 | 19,0 |
| Realistic | 4,4 | 9,1 | 16,5 |
| Ideal | 3,6 | 7,2 | 13,1 |
Table 4 Average promotion years at different career levels (organizational promotion policy)
5.3 Simulation of application evaluation mechanisms
The next step in model analysis was to consider the submodels related to application evaluation. There are essentially two independent mechanisms to be studied - the build up of the “objective” quality of the application based on intrinsic research skill and writing (i.e. non-research) skills and the actual selection outcome that is a function of the objective quality and evaluation error. It is plausible that both application quality and accuracy of evaluation depend on the time used but as we have no model for this dependency we fix the time budget and vary quality and accuracy parameters independently.
The “Realistic” scenario with 50% resource level, non monotonous frustration build up and lower variability of researcher skills was taken as basis (with \(1/10\)th of research time made available for writing and 5% reserved for administrative overhead). Research skill’s weight in the application quality varied from 20% to 100% and the weight of the evaluation error from 0% to 80%. The results are shown in Table 5 and Figure 2.
| Policy | SkillWeight/ErrorWeight | 0 | 0,2 | 0,4 | 0,6 | 0,8 |
| Individual | 0,20 | 325 | 327 | 328 | 319 | 301 |
| Individual | 0,40 | 367 | 367 | 360 | 335 | 306 |
| Individual | 0,60 | 407 | 408 | 389 | 346 | 308 |
| Individual | 0,80 | 433 | 423 | 399 | 357 | 309 |
| Individual | 1,00 | 436 | 416 | 393 | 355 | 316 |
| Organizational | 0,20 | 321 | 323 | 322 | 310 | 294 |
| Organizational | 0,40 | 357 | 355 | 347 | 328 | 296 |
| Organizational | 0,60 | 396 | 399 | 378 | 340 | 303 |
| Organizational | 0,80 | 423 | 416 | 387 | 350 | 307 |
| Organizational | 1,00 | 425 | 412 | 385 | 343 | 307 |
Table 5 Citation counts w.r.t weight or research skill (row) and evaluation error (column).
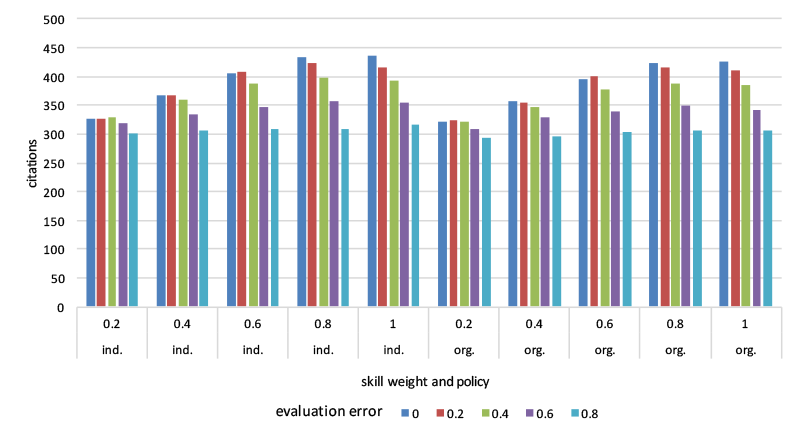
Fig. 2 Citation counts across skill research skills and evaluation error
The effects are quite insensitive to the promotion policy. Also it is seen that the grant allocation mechanism tolerates quite well small evaluation errors and moderate role of the writing skill. However, when the writing skill starts to dominate (research skill contributes at most 40%) the evaluation error loses its role and the results correspond to the lottery at most and eventually the performance degrades to worse than lottery due to the time sacrificed to application writing and evaluation. Naturally the lost time affects to the performance also in absence of evaluation error or bias. The ideal scenario with full resources leads to 495 + -5 citations. Thus writing and evaluation overhead leads to 15 - 20% drop in performance as expected (for selected parameters). Given that (for these parameters) lottery can reach up to 330 citations (65% of the ideal performance), the role of application overhead is significant as such and is further amplified by the bias and error in the selection.
5.4 Analysis of application writing time mechanism
As last case we consider the effect of reserving research time for application writing. The “Realistic” scenario with 50% resource level, non monotonous frustration build up and lower variability of researcher skills was again taken as basis. The roles of writing skill and evaluation error were set to 50%. No separate overhead for application evaluation was applied but evaluation was included in the preparation workload.
Half of the total research resource was allocated to grants and the rest distributed evenly to researchers to be available to preparing applications and making research. 0 to 90% of that time was nominally allocated for application writing depending on the current frustration level (higher frustration implies less time sacrificed to application and hence more time for writing papers).
The basic model behaviour is summarised in Table 6. Both paper and citation counts diminish when less time is available for research. Frustration and skill levels seem are insensitive to the amount of writing time. The break-even point to lottery is around 60% (i.e. 30% of the total research resource or 15% of the total working time).
If the variability of skills between researchers is higher (explaining 65% of the variance in papers’ quality) the outcome is bit less sinister. Then the break-even is around 36% of the research time or 18% of the working time.
| Writing intensity | Citations | Papers | Frustration | Skill |
| 0% | 416 | 88 | 32,3 | 113,3 |
| 10% | 400 | 85 | 32,3 | 113,6 |
| 20% | 387 | 82 | 32,6 | 113,6 |
| 30% | 372 | 79 | 32,6 | 113,7 |
| 40% | 356 | 75 | 32,7 | 113,5 |
| 50% | 346 | 72 | 32,6 | 114,2 |
| 60% | 329 | 69 | 32,8 | 113,5 |
| 70% | 310 | 66 | 32,8 | 113,1 |
| 80% | 300 | 63 | 33,0 | 113,4 |
| 90% | 285 | 60 | 33,1 | 113,9 |
Table 6 Model performance as function of nominal application writing time
6 Discussion
We have studied how simple statistical simulation can reveal the implications of different funding allocation mechanisms both to the system output (scientific impact) as well as to the internal state of the system and individual researchers. The results invite to more elaborate simulations and modelling of different phenomena which in its turn will require new scientometric data in order to achieve more quantitative predictions.
The very basic comparison of extreme scenarios (“communism”, “lottery”, “idealism” and “capitalism”) revealed subtle interactions between research funding and career build up as well as the question of productivity as function of resource allocation.
The two random allocation mechanisms produced similar average skill levels for the total population. This was expected as the funding allocation did not consider skills in any way. However, although the promotion mechanism had no direct dependency on obtained research funding or number of papers, different resource allocation mechanisms resulted to quite distinct personnel profiles. Hence, the promotion mechanisms can not be studied/used without being aware of the funding mechanisms and vice versa.
For the purpose of simulating the application based grant allocation we tacitly assumed that there exist two hidden qualities of a researcher. The one called research skill contributes both to application quality and the actual simulated scientific output whereas the other (writing skill) only affects the success in grant allocation.
Taking the utilitarian view that the grant allocation aims to maximize the scientific impact of the research community we can interprete both the role of (application) writing skill and the actual evaluation error as defects in the grant allocation. While these two mechanisms have similar effects to the scientific impact (citations) they have different influences to the personnel dynamics. Unpredictable evaluation errors have more adverse effect to the motivation of the researchers and hence to their paper output. Evaluation errors also give more possibilities to mediocre young researchers to focus on research and be promoted leading to more stagnated staff profile. More deterministic selection mechanism leads to systematic funding and eventual promotion of researchers having good combination of writing and research skills.
Qualitatively our model is credible - each selection process will introduce some artificial criteria that are not directly linked to the intrinsinc scientific potential of the applicant. A completely different question is how the research skill and writing skill scale and compare together or with the evaluation error and how the real selection mechanisms work (like first preselection of good enough scientific content and then a "political" final round - or vice versa, first formal consistency check and after that a peer review of the short list).
Despite of rather rudimentary model for frustration the interactions between funding decisions, motivation and productivity could be observed, in particular in personnel profiles. The main observable, system throughput in citations (as function of resource allocation), was, however, not very sensitive to different frustration and promotion models.
Finally, the question that is of interest to the whole community of researchers: what can we say about the balance between the time invested in the application excercise and the accuracy in targeting the research funding. The simulation results suggest that it will not pay off to try to reach high accuracy in selection if it requires more investment to application writing and evaluation. It is enough that scientific quality is in par with other qualities and evaluation errors (given that all have similar statistical behavior). The loss of research potential due to application overhead is quite obvious. What was more surprising was the relative robustness of the system to tolerate significant bias and errors in grant evaluation. This can partly be due to simulated yearly allocation of research time that averages out random errors and partly due to idealized promotion policy that takes into account only the scientific impact shown by citations and ignores local politics. Reality may be quite different in this respect.
7 Conclusions
We implemented a conceptually simple simulation model that describes qualitatively the interactions between the grant allocation process, organisation’s promotion process, researcher’s skill, motivation and productivity.
While the individual mechanisms were chosen quite simple and were observed to behave in expected and understandable way the real value of simulations comes from revealing the complexity of interactions between different mechanisms.
Grant allocation mechanisms interact with promotion mechanism leading to quite different personnel dynamics depending if the grant allocation is systematic but biased or if the allocation is unbiased but has significant inherent randomness. Grant allocation affects also the frustration and motivation levels in the population. Randomness in allocation is prone to give more possibilities to less skilled staff and lowering the morale of the skilled staff whereas more systematic allocation divides the population quite systematically to winners and losers and leading to higher overall volatility in the staff due to faster rotation of researchers with less favoured skill profile.
Different grant allocation mechanisms make the difference in the overall performance mainly by enabling different researchers to work and publish to be successfull in promotions. This causes both the head count and skill profiles at different career levels to vary depending on the grant allocation schemes.
The source code of PEGS is available at www.bartneck.de/publications/2016/PEGS/index.html.
7.1 Limitations and further research
The reported simulations are done for one closed scientific community (mimicking a national academic system as a whole). Hence they do not consider competing organisations and mobility between them. Likewise, we consider only individual researchers doing solitary work and no attempt is made to model team work with joint publications or joint applications. Also there is only one grant allocation mechanism with one set of rules and running yearly.
In reality there are always several mechanisms contributing to allocation of research time ranging from the individual sacrifices of evenings and weekends via work arrangements at department level to actual grant instruments available on institute and system level. In order to consider particular grant allocation schemes the applied formal or implicit grading systems have to be analyzed. There may be categories that can easily be identified with "writing skills", for example. Also the funding bodies in question might have data on the distribution of evaluations given by different experts to the same application (to get a measure for the evaluation error). Hence, it is at least plausible that this part of the simulation model could be calibrated to a given system.
Before getting this kind of data it is difficult to derive quantitative estimates for the tradeoff of investing more time to more elaborate applications to reduce the evaluation error. This question is critical as the payoff from ideal grant selection is always finite compared to random lottery type allocation and the payoff is easily lost by evaluation errors and biases due to selection technique.
The researchers are modeled quite simplistically - having only two constant personal characteristics (research and writing skills). The rest of the properties (like frustration dynamics, activity in applying, productivity, etc) are the same for the whole population. These could easily be made to vary but this will lead to need of identifying new distributions lacking empirical data. Also at present the researcher is ignorant of her relative personal skill level as well as the selection rules when allocating time to writing applications. If different funding mechanisms and different organisations are introduced (with different rules and HR policies) more elaborate model on researchers will be needed. This would also give the possibility of trying to model the possible bias in selection process towards certain personality types. Moreover, PEGS is currently not able to model differences between scientific disciplines and countries.
For productivity and quality of publications there is empirical data that has not yet been exploited fully in simulation. Without a model for the collaboration and joint publications there is no point in trying to fit the distribution of the actual publication count. So we have aggregated researcher’s productivity in the research skill only. From the point of view of simulation results only the cumulative citation count is important (be it obtained with few good or several mediocre papers). The parameters like immediacity and longevity in the model of Wang et al are likely to have an impact in the simulation results, especially if we assume that these may vary as researcher’s personal properties (like the skill/fitness).
The reported simulations were done under the assumption that ability to focus to research for longer periods (within an academic year in our simulation) did not boost productivity. This was crucial in comparing communistic scenario to the others. How valid this assumption is, is a relevant question that could perhaps be answered with access to time allocation data of researchers that could be combined to the publication data.
References
- Afonso A (2013) How academia resembles a drug gang. URL http://alexandreafonso.wordpress.com/2013/11/21/how-academia-resembles-a-drug-gang/
- van Arensbergen P, van der Weijden I, van den Besselaar P (2012) Gender differences in scientific productivity: a persisting phenomenon? Scientometrics 93(3):857–868, DOI 10.1007/s11192-012-0712-y
- Barnes LLB, Agago MO, Coombs WT (1998) Effects of job-related stress on faculty intention to leave academia. Research in Higher Education 39(4), 457-469
- Barnett A, Herbert D, Graves N (2013) The end of written grant applications: let's use a formula URL http://theconversation.com/the-end-of-written-grant-applications-lets-use-a-formula-19747
- Bartneck C (2010) The all-in publication policy. In: Fourth International Conference on Digital Society (ICDS 2010), IEEE, St. Maarten, pp 37–40, DOI 10.1109/ICDS.2010.14
- Bazeley P (2003) Defining 'early career' in research. Higher Education 45(3), 257-279
- Canterbury University - Human Resource Department (2013) Staff report, human resources department of canterbury university, New Zealand
- Carayol N, Mireille M (2004) Does research organization influence academic production?: Laboratory level evidence from a large european university. Research Policy, 33(8), 1081–1102. doi:10.1016/j.respol.2004.03.004.
- Curtis JW, Thornton S (2013) The annual report on economic status of the profession. Academe 99(2), 4–17
- Day NE (2011) The silent majority: Manuscript rejection and its impact on scholars. Academy of Management Learning & Education 10(4):704–718, DOI 10.5465/amle.2010.0027
- Duckworth AL, Peterson C, Matthews MD, Kelly DR (2007) Grit: Perseverance and passion for long-term goals. Journal of Personality and Social Psychology 92(6):1087 – 1101
- Economic, Council SR (2010) Success rates. URL http://www.esrc.ac.uk/about-esrc/mission-strategy-priorities/demand-management/success-rates.aspx
- Engineering and Physical Sciences Research Council (2013) Success rates. Tech. rep., URL http://www.epsrc.ac.uk/funding/fundingdecisions/successrates/201213/
- Franceschet M (2009) A cluster analysis of scholar and journal bibliometric indicators. Journal of the American Society for Information Science and Technology, 60(10), 1950–1964
- Friesenhahn I, Beaudry C (2014) The global state of young scientists. Tech. rep., URL http://www.globalyoungacademy.net/projects/glosys-1/gya-glosys-report-webversion
- Funken C, Hörlin S, Rogge JC (2014) Generation 35 plus - aufstieg oder ausstieg? Tech. rep., Technische Universität Berlin, URL https://www.mgs.tu-berlin.de/fileadmin/i62/mgs/Generation35plus_ebook.pdf
- Geard N, Noble J (2010) Modelling academic research funding as a resource allocation problem:Proceedings of the 3rd World Congress on Social Simulation, University of Kassel, Germany (pp. SES-09_I).
- GEW, German Education Union (2014) The templin manifesto URL http://www.gew.de/Binaries/Binary90289/Templin_Manifesto.pdf
- Hattie J, Marsh HW (1996) The relationship between research and teaching: A meta-analysis. Education & Educational Research, 66, 507–542.
- Herbert DL, Coveney J, Clarke P, Graves N, Barnett AG (2013) On the time spent preparing grant proposals: an observational study of australian researchers. BMJ Open 3(5), doi:10.1136/bmjopen-2013-002800
- Herbert DL, Coveney J, Clarke P, Graves N, Barnett AG (2014) The impact of funding deadlines on personal workloads, stress and family relationships: a qualitative study of australian researchers. BMJ Open 4(3), DOI 10.1136/bmjopen-2013-004462
- Ioannidis JPA, Boyack KW, Klavans R (2014) Estimates of the continuously publishing core in the scientific workforce. PLoS ONE 9(7):e101,698, DOI 10.1371/journal.pone.0101698
- Johnsrud LK, Rosser VJ (2002) Faculty members’ morale and their intention to leave: A multilevel explanation. The Journal of Higher Education 73:518–542
- Jones A (2013) The explosive growth of postdocs in computer science. Communications of the ACM, 56,37–39. doi:10.1145/2408776.2408801.
- Kelchtermans S, Veugelers R (2005) Top research productivity and its persistence. a survival time analysis for a panel of belgian scientists. DTEW Research Report 0576 pp 1–31, DOI 10.1089/dst.2013.0013
- Knapp LG, Kelly-Reid JE, Ginder SA (2011) Employees in postsecondary institutions, fall 2010, and salaries of full-time instructional staff, 2010-11. Tech. rep., U.S. Department of Education
- Koelman J, Venniker R (2011) Public funding of academic research: The research assessment exerciseof the UK. In Higher education reform: Getting the incentives right (pp. 101–117). Den Haag: SDU.
- van der Lee R, Ellemers N (2015) Gender contributes to personal research funding success in the netherlands. Proceedings of the National Academy of Sciences 112(40):12,349–12,353, DOI 10.1073/pnas.1510159112
- Link AN, Swann CA, Bozeman B (2008) A time allocation study of university faculty. Economics of Education Review 27(4):363 – 374, DOI 10.1016/j.econedurev.2007.04.002
- Moses I (1986) romotion of academic staff: Reward and incentive. Higher Education (15):135–159
- National Health and Medical Research Council of Australia (2013) Annual report 2012-2013 National Institute of Healt (2013) Success rates. URL http://report.nih.gov/success_rates/
- Peyton SJ, Bundy A (2006) Writing a good grant proposal. URL http://research.microsoft.com/en-us/um/people/simonpj/papers/proposal.html
- Rice C (2014) Why women leave academia and why universities should be worried. URL http://www.theguardian.com/higher-education-network/blog/2012/may/24/why-women-leave-academia
- Roey S, Rak R (1998) Fall staff in postsecondary institutions, 1995. Tech. rep., U.S. Department of Education, Office of Educational Research and Improvement
- Tertiary Education Comission (2012) Performance-based research fund evaluating research excellence—the 2012 Assessment (Interim Report). http://www.tec.govt.nz/Documents/Reports%20and%20other%20documents/PBRF-Assessment-Interim-Report-2012.pdf.
- Wang D, Song C, Barabasi AL (2013) Quantifying long-term scientific impact. Science 342(6154):127–132, DOI 10.1126/science.1237825
This is a pre-print version | last updated July 7, 2016 | All Publications